マンデルブロのフラクタルとか、カオス理論、バタフライ効果、べき乗則など…
何やら"複雑系"という分野で、ひとまとめにできるようだけど位置づけが???
11年も昔の本だから微妙だけど、イメージとしてつかみやすかったのはこれ。
マーク・ブキャナン「歴史はべき乗則で動く」は、
地震や種の絶滅といった自然現象から、株価や所得分布といった社会現象まで、
様々な面で「べき乗則」が成り立っていることを解説してくれる興味深い本。
株価変動の大きさが2倍になると、その頻度は16分の1になるという研究がある。
べき乗則を使えば、効率的市場仮説を否定するのは簡単みたい。
「効率的市場仮説のより所となっている前提とはまったく逆に、市場株価の大きな変動は市場におのずから内在する作用の結果であり、それは「構造的な脆弱性」や基礎条件の突然の変化などなくても、しばしば起こることである。その理由は単純だ。市場は平衡状態から遠く隔たっているからだ。」P230
初めは、べき乗則?なんじゃそりゃ?と思ったが、
ロングテールでおなじみのパレートの法則やファットテールもべき乗則らしい。
また、正規分布とべき乗則の違いが、一目で分かる図があった。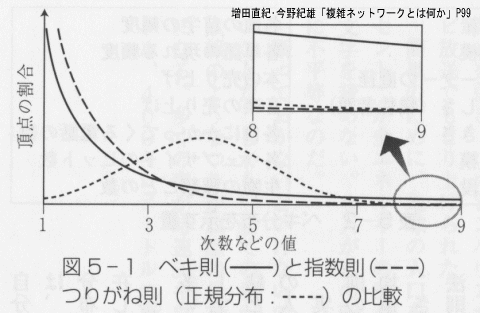
複雑系と投資を絡めた本として、マイケル・モーブッシン「投資の科学」
があることをすっかり忘れていた。もう一度読んでみなければ。


コメント
複雑系って知らないんですが、べき乗の法則ですか・・・。
そういえば地震の大きさを表すマグニチュードや一般に音の大きさを表すデシベル(dB)も10^Xの関係なんですよね。
べき乗の法則が、フラクタルや自己組織的臨界状態(←それが何か分かっていない)の土台になってるらしいです。だからとりあえず、べき乗の話の本から読んでいくと、複雑系に近づけるのかなぁ、と模索中なのです。
複雑系は懐かしいですね。私も昔よく読んだ覚えがあります。
一般的な複雑系入門書、としてはMitchell Waldrop氏の
COMPLEXITY(まんまですな)が読みやすかった記憶があります。全然投資とは関係ないですが。。
未だにサンタフェの専門研究機関は稼働中のようです。
(設立にあのケネスアローもかかわってます)
http://www.santafe.edu/
ご紹介頂いた本、日本語訳が出ているようなので、図書館で借りて読んでみます。ありがとうございます。(Amazonで売ってないのは人気がないから???)
あと最近、クルーグマンの経済学と複雑系を絡めた「自己組織化の経済学」って本を見つけたので読んでいます。